Design and Reliability Research of Spherical Radiotherapy Accelerator Motion System
-
摘要:
目前，放射治疗设备常用的C形臂结构加速器在实现非共面治疗时，操作复杂且存在安全隐患。该文结合医用机械臂技术设计了一种球面放疗加速器运动系统，通过医用机械臂结构夹持束流模块，实现非共面范围的立体多角度照射治疗。首先，对球面放射治疗设备的旋转机架、束流模块和MLC模块进行结构设计；其次，采用双平面配重法对设备进行动平衡计算，保证射束中心点在治疗过程中不会发生旋转偏移；最后，对传动部件齿轮进行强度校核及可靠性分析。结果表明，该文设计的球面放疗加速器运动系统可满足精确放疗稳、准、快的要求，有助于提高治疗效率。
Abstract:At present, the C-arm structure accelerators commonly used in radiotherapy equipment are complex in operation and have potential safety hazards when realizing non-coplanar treatment. By combining with medical robotic arm technology, a spherical radiotherapy accelerator motion system is designed. The beam module is clamped by the medical robotic arm structure to achieve three-dimensional multi-angle irradiation treatment within the non-coplanar angle range. Firstly, the rotating mechanism, beam module, and MLC module of the spherical radiotherapy equipment are designed. Then, the double-plane counterweight method is used to calculate the dynamic balance of the equipment, ensuring that the beam center point does not rotate during the treatment process. Finally, the strength check and reliability analysis of the transmission component gear are conducted. The results show that the designed spherical radiotherapy accelerator motion system can meet the requirements of stable, accurate, and fast precision radiotherapy, which is conducive to improving the treatment efficiency.
-
0. 引言
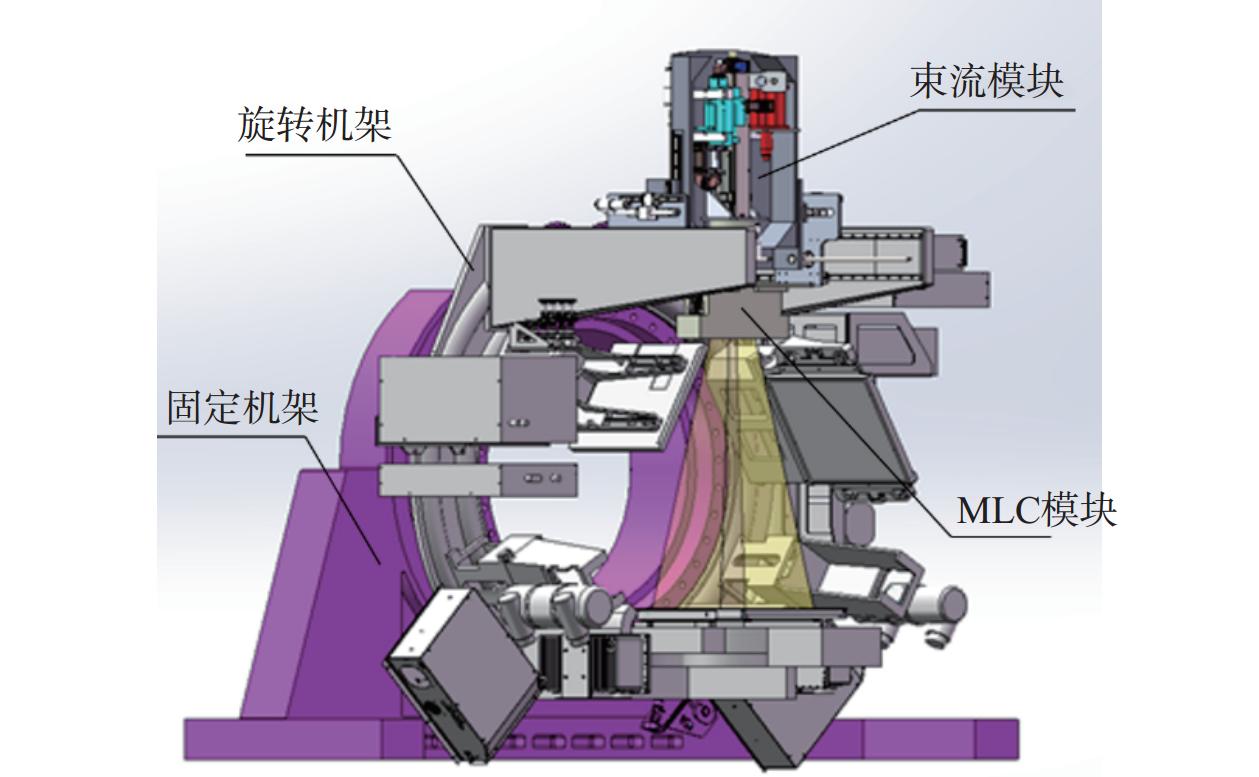
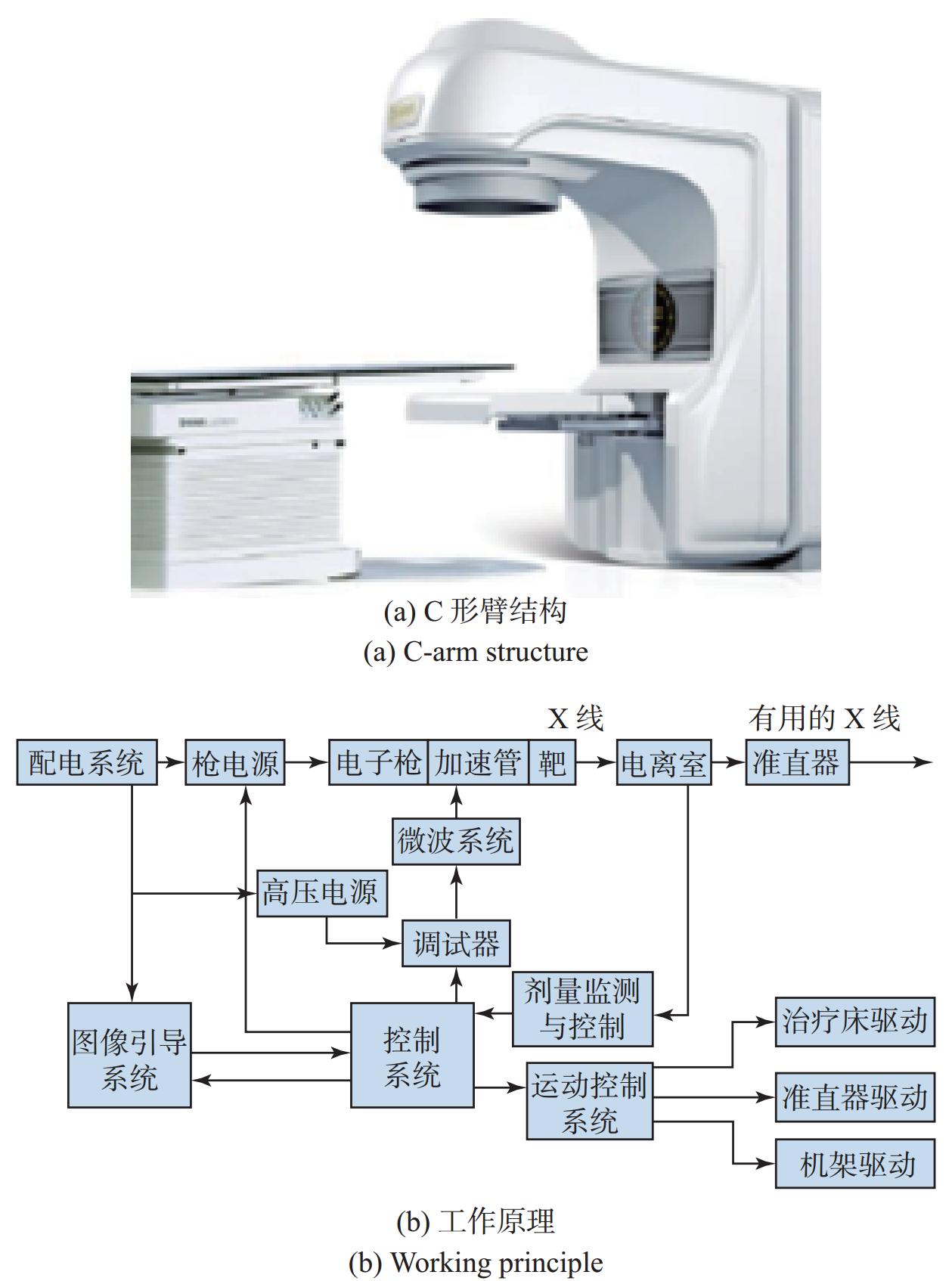
肿瘤已成为世界各国的常见病和多发病。目前，针对肿瘤疾病的治疗手段有手术治疗、化学治疗、生物反应调节剂治疗、中医治疗及放射治疗等[1]。放射治疗是通过高能辐射消灭癌细胞或阻止癌细胞扩散的一种治疗癌症的方法[2]。随着图像引导技术和计算机技术等的发展，放射治疗现在已经成为治疗肿瘤的主要手段之一[3]。国际原子能机构（International Atomic Energy Agency, IAEA）发布的数据显示[4]，世界上医疗理念先进以及高收入的国家拥有较多的放射治疗设备，患者采用放射治疗的比例也较高，其中美国高达63%，瑞典、荷兰等西方国家均超过40%，而我国患者采用放射治疗的比例不足30%。受限于国外厂商的垄断，我国国产放射治疗设备市场占有率不足10%。《中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要》明确提出要大力发展放射治疗设备，加快放射治疗设备的国产化替代过程，增加放射治疗设备产量[5]。放射治疗设备是一种集成计算机技术、放射技术、分子成像技术的设备。目前国内采用的放射治疗设备多为C形臂结构，如图1a所示，该结构占用空间大，在进行非共面照射时操作复杂，需要操作人员进入治疗间调整加速器位置，存在安全隐患，同时增加治疗时间，降低效率。
为了实现非转床方式的非共面照射，提高治疗效率与空间利用率等，本研究团队在近年来新兴的质子治疗的基础上[6]，提出了一种将医用机械臂应用于放射治疗设备的结构设计。该设计兼顾灵活性、空间利用率高等优点，同时解决了赛博刀只能实现半球定点照射且无法高效拉弧的问题，实现了头部和体部的立体多角度照射，达到降低靶区周围正常组织和器官剂量、提高靶区剂量的目的。此外，对设计的放射治疗设备进行动平衡计算，以保证设备的稳定性；进行结构仿真，验证结构的刚度和强度满足要求，确保设备能够投入正常使用。
1. 放射治疗设备工作原理及结构设计
医用直线加速器主要由机械系统、束流模块系统、运动控制系统及图像引导系统等组成[7]。其利用微波电场对带电粒子加速得到较高的能量，之后可使用高能电子直接进行治疗，或者通过高能电子轰击不同材料的靶，得到所治疗肿瘤细胞的粒子束。医用直线加速器的工作原理如图1b所示。
1.1 整体结构设计
放射治疗设备的整体结构设计如图2所示，主要包括固定机架、旋转机架、束流模块和多叶光栅（multi-leaf collimator, MLC）模块。固定机架的底部固定在地面上以保证整体设备的稳定性。通过在旋转机架上安装球管、高压控制箱、屏蔽体和平板探测器等组件，提高空间利用率。以旋转机架的圆心为旋转中心，各个部件相对于旋转中心具有合理的距离，以保证放射治疗设备具有良好的通风性，在不同操作状态下，能够确保空气温度的稳定和有害气体的充分排出。旋转机架通过齿轮副进行驱动，带动各组件完成圆周运动。束流模块和MLC模块主要由机械臂带动完成3个方向的运动。操作人员在控制室通过操控机械臂的运动，对射束的位置进行调整，实现放射治疗设备以非转床方式进行非共面照射，提高医疗效率，减少安全隐患。
1.2 旋转机架的设计
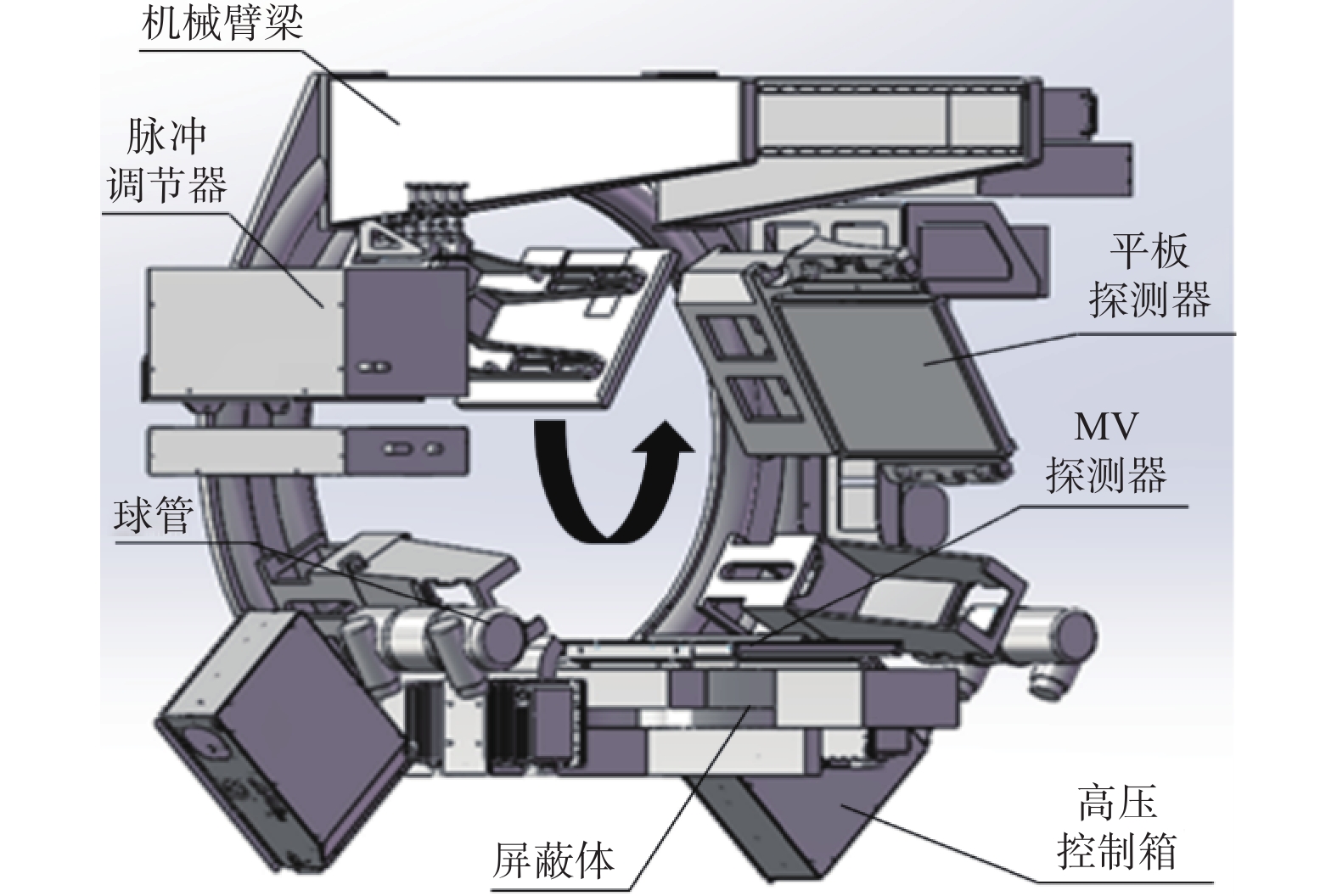
本文提出利用一种旋转机架代替现有的C形臂结构的方案，完成对放射治疗设备部件的承载和旋转运动。通过交流伺服电机连接减速器驱动齿轮，使旋转机架完成以逆时针为正方向的绕Y轴的圆周旋转运动。为了在治疗过程中提高医疗效率，减少中途操作时间，在旋转机架上安装了平板探测器、高压控制箱和屏蔽体等部件，并集成了计算机和分子成像等技术。旋转机架的设计如图3所示。应合理安装各个组件并设置安全距离，保证其具有充足的工作空间。安装的影像监视、对讲系统等组件要保证在照射前及照射过程中，操作人员可以无阻碍地观察到患者，并在有需求的情况下和患者交流，保证操作人员在控制室观察到整个治疗过程，从而及时调整设备，减少治疗过程中进出治疗室调整设备的情况。
1.3 束流模块和MLC模块的运动设计
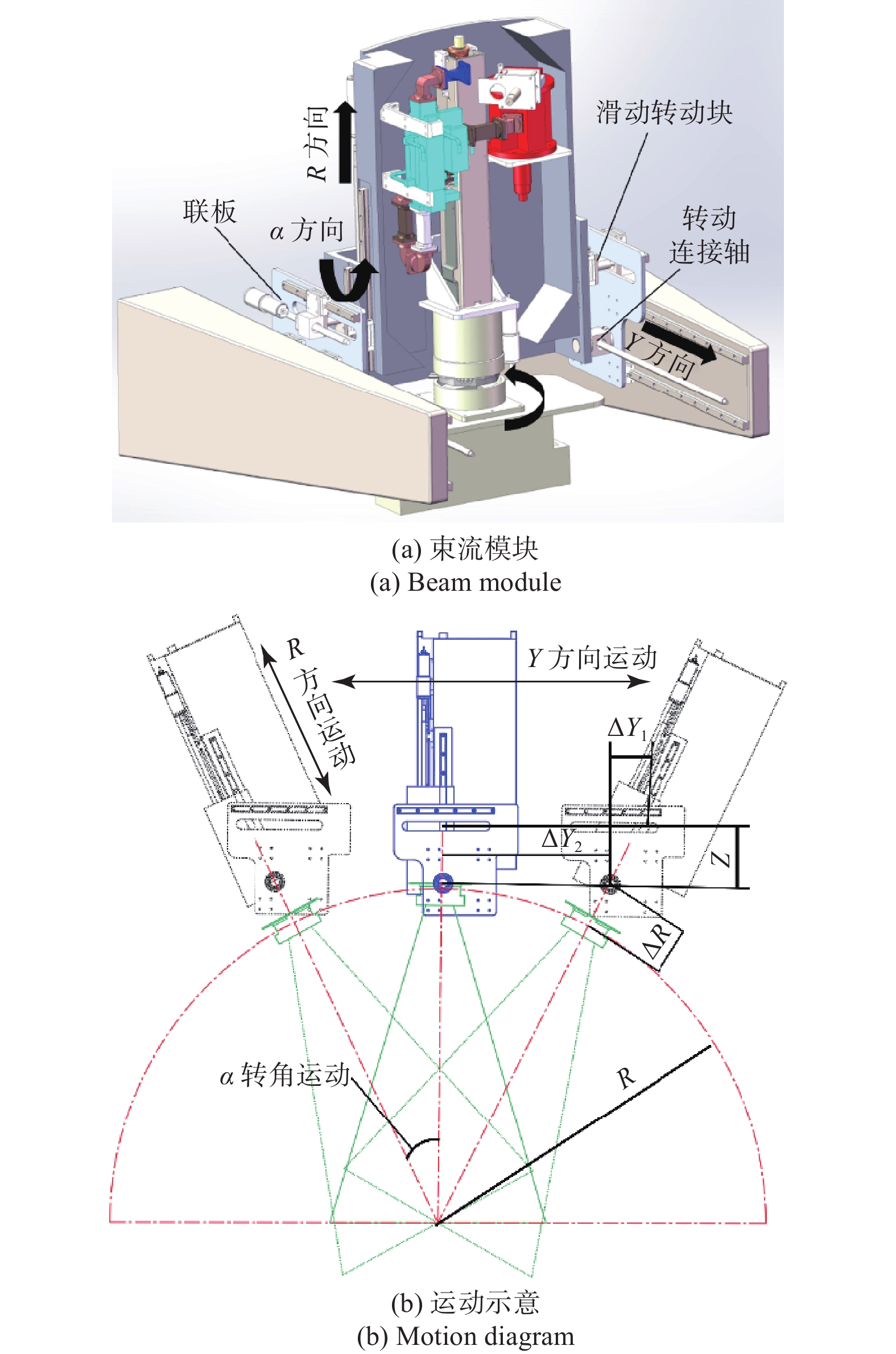
夹持束流模块的机械臂结构可以实现3个方向的运动。在Y方向以治疗床脱离放射治疗设备的方向为正方向的水平平移往复运动，行程为
1158 mm；在R方向以径向方向上远离旋转机架圆心为正方向的往复平移运动，行程为458 mm；在α方向以束流模块沿径向逆时针摆动为正方向的往复转角运动，运动角度为30°。通过在联板上安装旋转连接轴和滑动转动块，共同驱动完成转角运动。MLC模块可以实现以逆时针为正方向的绕自身中心轴线的圆周旋转运动。束流模块及运动示意如图4所示。图中$\Delta R $为R方向偏移量，$\Delta Y_1 $和$\Delta Y_2 $为电机转动圈数。束流模块和MLC模块中各方向的运动均采用交流伺服电机直连滚珠丝杠驱动完成。束流模块和MLC模块沿Y方向的往复平移运动，实现了射束对人体从头部到体部的Y方向上完整的照射扫描；沿R方向的运动可使射线源与靶点始终保持相同的距离，弥补了由于旋转机架在旋转过程中角度偏移导致的径向方向上的距离偏差，保证射束剂量的精准性；沿α方向的倾角摆动实现了射束的非共面照射，达到了将有用剂量从更多角度向靶区聚集的目的，提高了放射治疗效率。MLC模块沿自身轴线所做的圆周旋转运动使射束更好地贴合靶区，从而完成精准打击，减少对癌细胞周围正常组织和器官的伤害。
2. 可靠性研究
2.1 动平衡设计
放射治疗设备旋转机架上的负载部件多且质量差距较大。在旋转过程中，动不平衡引起的振动会使照射区域产生偏移，导致治疗区域所接受的放射剂量不稳定从而影响治疗效果。不均匀振动引起的噪声会给患者的心理状态与医护人员的工作环境造成影响，并且会降低部件的使用寿命。由于放射治疗设备对精度有极高的要求，所以要通过配重方法对设备进行动平衡的计算。目前，在机械设计中常用的配重方法[8]主要分为以下6种：质量块配重法、恒力弹簧法、磁性弹簧法、传统机械式拉簧法、氮气平衡器法及气缸平衡法（包括普通气缸法和钢绳气缸法）。综合考虑这6种方法的优缺点后，本文最终选取质量块配重法计算动平衡。
首先通过Solidworks中的质量属性设定旋转机架上加载的各个部件的质量和材料，再通过添加传感器测量重心，得到相对于旋转机架圆心的旋转半径和角度。部分部件的质量及旋转半径如表1所示。
表 1 部分部件的质量及旋转半径Table 1. Weight and radius of rotation of some parts序号 部件名称 质量/kg 旋转半径/mm 角度/(°) 1 平板探测器 26.3 607.45 29 2 脉冲调节器 137 1032.44 14 3 球管支架组1 34.9 963.36 330 4 高压控制箱1 26 1130.88 316 5 屏蔽体 872 661.37 271 6 栅控枪及电源 5 1255.5 136 7 束流模块 381 902.31 86 利用双平面配重法对设备进行动平衡设计，选定两个配重平面，选定配重块的旋转半径为旋转机架的半径。将各个部件质径积折合到选定的两个平面后，进行矢量和的运算。配重平面质径积的计算如式(1)和式(2)所示[9]。
$$ {MD}_{i'}=\frac{{L}_{2}-{Z}_{i}}{{L}_{2}-{L}_{1}}\cdot {m}_{i}\cdot {r}_{i}$$ (1) $$ {MD}_{i''}=\frac{{Z}_{i}-{L}_{1}}{{L}_{2}-{L}_{1}}\cdot {m}_{i}\cdot {r}_{i}$$ (2) 式中：${\textit{MD}}_{i'} $为配重平面1内各部件质径积；${\textit{MD}}_{i''} $为配重平面2内各部件质径积；L2为配重平面2的Z轴坐标；L1为配重平面1的Z轴坐标；mi为各部件质量；ri为各部件旋转半径。
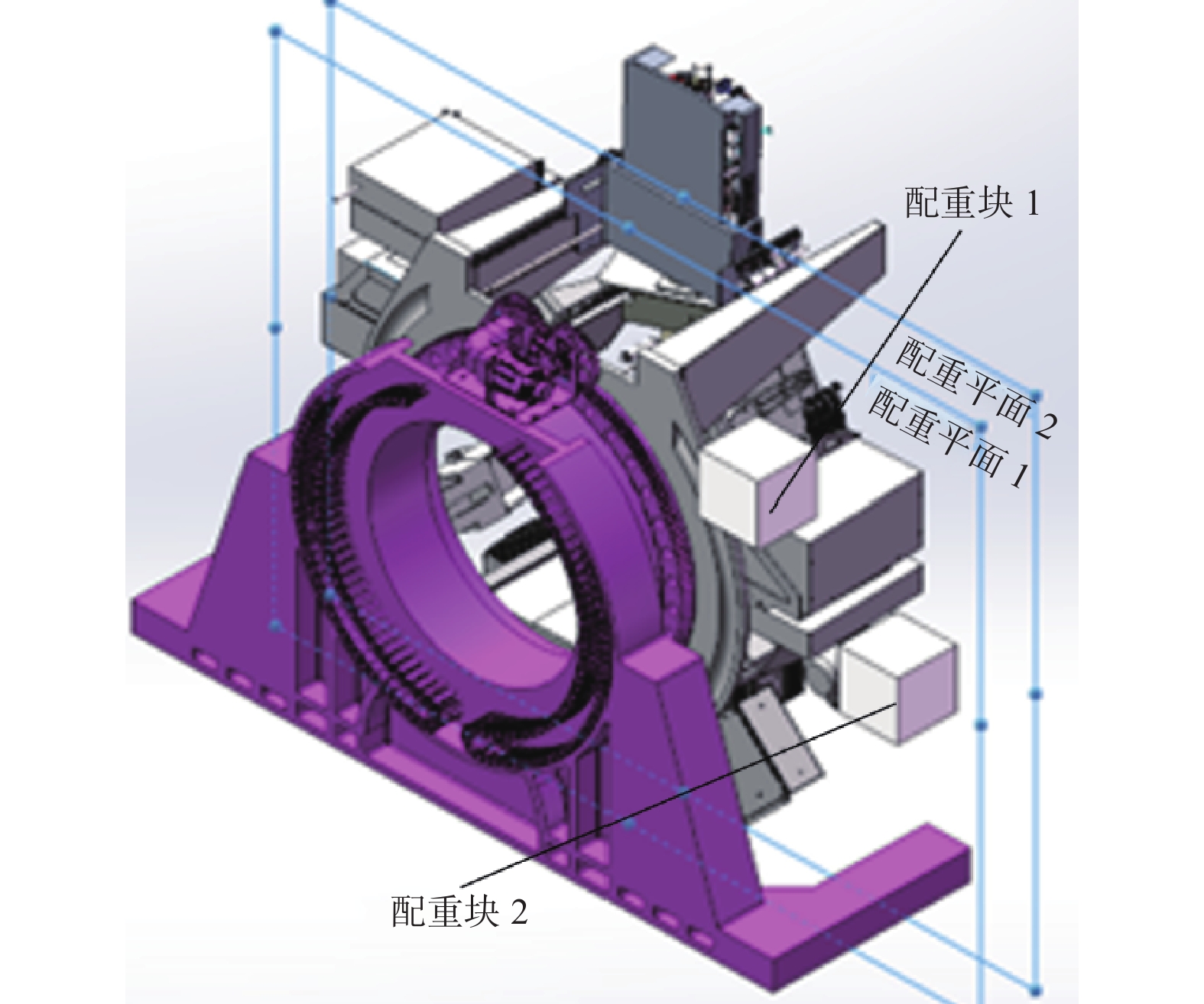
配重平面质径积根据配重平面内质径积矢量和为零进行计算，得到需要补偿的两个配重块质量分别为436.7 kg和142 kg。配重块的位置如图5所示。将计算得到的配重块添加到Solidworks软件中，进行motion仿真。仿真结果为优化后的动平衡中心偏移。X、Y、Z方向的线性偏移误差分别为(1.0±0.4) mm、(0.8±0.4) mm、(0.4±0.4) mm，文中X、Y、Z方向均参考IEC 61217标准定义的坐标系。故配重后的加速器系统可以正常平稳运行。
2.2 机械臂梁的可靠性研究
机械臂梁作为承载束流模块的关键部件，对其进行可靠性研究是有必要的，由于孔、圆角等特征对静态分析结果影响较小，故对模型作简化处理。将模型保存为parasolid格式导入Workbench软件中，使用DesignModeler模块作细致处理。根据束流模块的质量及材料属性设定模型的接触边界条件，限定整个网格划分单元大小为20 mm，采用六面体网格划分方法。机械臂梁变形云图如图6所示。
从图6中可以看出机械臂梁未出现变形严重、应力过大或应力集中的现象。机械臂梁的最大变形量为0.47 mm，最大变形出现在机械臂梁的最前端；最大应力为104.37 MPa，远小于40CrMo的屈服强度930 MPa，满足使用要求。
2.3 齿轮的可靠性研究
2.3.1 齿轮的参数化建模及网格划分
标准直齿轮的齿廓曲线为渐开线，确定齿轮的渐开线是建模的关键所在。基于Solidworks软件中的表达式绘制齿轮的渐开线，之后进行二维齿面的绘制，通过绘制齿根圆、基圆、分度圆和齿顶圆，完成齿轮的初步绘制过程。部分齿轮参数如表2所示，齿轮副模型如图7所示。
表 2 部分齿轮参数Table 2. Parts of gear parameters齿轮 模数 齿数 压力角
/(°)齿顶圆
/mm齿根圆
/mm分度圆
/mm小齿轮 8 30 20 256 220 240 大齿轮 8 180 20 1456 1420 1440 选取Workbench软件中的瞬态模块分析齿轮，根据所设计齿轮的尺寸和瞬态模块的分析特性修改模型，选取小齿轮的完整模型、大齿轮1/10齿数的模型进行仿真分析。网格划分采用三维扫掠映射方法，对齿轮副中参与接触分析的齿做局部加密处理，采用缓慢过渡方法以保证网格质量。接触算法选取增强拉格朗日乘子法，其对接触刚度敏感度低，容易得到良态条件。
2.3.2 齿轮的理论强度校核计算
从静态校核方面分析齿轮，经过简化的齿面接触强度计算方法如式(3)所示[10]。
$$ \sigma_H=Z_EZ_HZ_{\varepsilon}\sqrt{\frac{2K\boldsymbol{T}_1}{bd_1^2}\cdot\frac{u\pm1}{u}}\leqslant\left[\sigma_H\right] $$ (3) 式中：ZE为弹性系数；ZH为节点区域系数；Zε为重合度系数；T1为输入转矩；K为载荷系数；b为圆柱体接触长度；d1为节圆直径；u为齿数比。其中：
$$ K={K}_{A}{K}_{V}{K}_{\alpha }{K}_{\beta } $$ (4) $$ {Z}_{\varepsilon }=\sqrt{\frac{4-{\varepsilon }_{\alpha }}{3}}$$ (5) $$ {Z}_{E}=\sqrt{\frac{1}{\text{π} \left(\dfrac{1-{\mu }_{1}^{2}}{{E}_{1}}+\dfrac{1-{\mu }_{2}^{2}}{{E}_{2}}\right)}} $$ (6) $$ {Z}_{H}=\sqrt{\frac{2}{{\mathrm{cos}}^{2}\alpha \cdot \mathrm{tan}\alpha '}}$$ (7) 式中：KA为使用系数；KV为动载荷系数；Kα为齿间载荷分配系数；Kβ为齿向载荷分配系数；μ1、μ2为不同齿轮泊松比；E1、E2为不同齿轮弹性模量；α为分度圆压力角；α'为啮合角。计算可得ZE=192.6，ZH=2.5，Zε=0.87，将数值代入式(3)，计算发现齿轮接触强度为299 MPa，小于齿轮的许用接触应力，说明齿轮的接触强度比较合适。
校核齿轮的齿根弯曲疲劳强度，简化后的计算方法如式(8)所示[11]。
$$ \sigma_F=\frac{K\boldsymbol{F}_t}{bm}\cdot Y_{Fa}\cdot Y_{Sa}\cdot Y_{\varepsilon}\leqslant\left[\sigma_F\right] $$ (8) 式中：K为载荷系数；Ft为圆周力的切向力；b为圆柱体接触长度；m为模数；YFa为齿形系数；YSa为应力修正系数；Yε为重合度系数。其中：
$$ {Y}_{\varepsilon }=0.25+\frac{0.75}{{\varepsilon }_{\alpha }} $$ (9) $$ {Y}_{Fa}=\frac{6\left(\dfrac{l}{m}\right)\mathrm{cos}\;{\alpha }_{F}}{{\left(\dfrac{s}{m}\right)}^{2}\mathrm{cos}\;\alpha }$$ (10) $$ {\varepsilon }_{\alpha }=\left[1.88-3.2\left(\frac{1}{{Z}_{1}}\pm \frac{1}{{Z}_{2}}\right)\right]\mathrm{cos}\;\beta $$ (11) 式中：l为弯曲力臂长度； αF为齿根应力；s为齿厚；m为模数；Z1、Z2为不同齿轮当量齿数； β为螺旋角。查询外齿轮齿形系数、外齿轮应力修正系数，得到YFa=2.52，YSa=1.63，Yε=0.93，将数值代入式(8)，计算得出齿根弯曲疲劳强度为207 MPa，小于许用弯曲应力，较为合适。
2.3.3 齿轮的强度校核仿真验证
结合现有放射治疗设备的运行条件，设定本文所用模型的边界条件的定义和加载方式。小齿轮和大齿轮均约束其中心位置，保证其只绕着轴心转动。小齿轮作为主动轮，对其施加力矩；大齿轮作为从动轮，对其施加转速。
在相同的时间点下，不同网格密度模型的接触应力值变化不大。齿轮在不同时间下的最大接触应力如表3所示，可以认为在局部加密网格的情况下，计算结果与网格数量不相关。
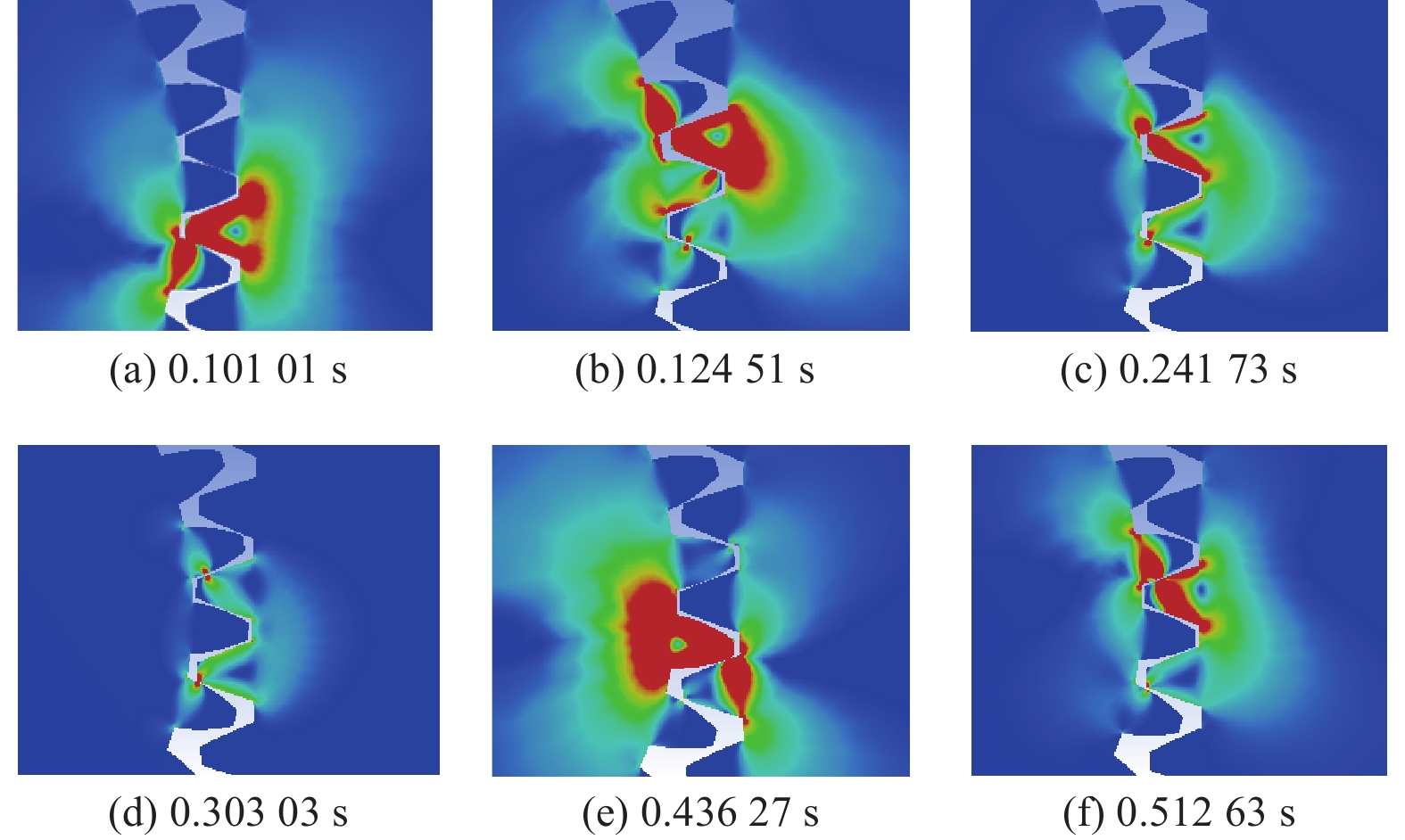
表 3 齿轮在不同时间下的最大接触应力Table 3. Maximum contact stress of gear at different time单位：MPa 时间/s 0.2465 0.5015 0.7465 0.9851 模型a 75 260 380 162 模型b 62 254 370 192 模型c 68 225 357 197 对齿轮求解得到齿轮部分啮合位置的等效应力云图，如图8所示；各啮合位置最大接触应力如表4所示。齿轮啮合时的接触应力呈现规律性变化，其最大接触应力满足使用要求。
![]()
图 8 齿轮副部分啮合位置等效应力云图Figure 8. Equivalent stress cloud diagram of partial meshing position of gear pair表 4 齿轮各啮合位置最大接触应力Table 4. Maximum contact stress at each meshing position of gear单位：MPa 图号 a b c d e f 啮合位置 单齿 啮入 双齿 双齿 啮出 单齿 最大接触应力 172 326 72 48 398 126 因为双齿啮合时接触应力由两对齿轮分担，齿轮的啮合刚度较高，所以双齿啮合时的最大接触应力要小于单齿啮合时的最大接触应力。可发现在齿轮啮入啮出过程中，齿轮的最大接触应力会发生较大变化，这是由于在啮合过程中齿轮的弹性变形会导致齿轮啮合区域产生偏差，导致从动轮与主动轮发生干涉，齿轮之间产生啮合冲击，从而使接触应力大幅上升。在实际生产过程中，可通过齿顶修型法或选取更合适的齿轮顶隙系数避免干涉现象的发生。
2.3.4 齿轮的啮合刚度分析
齿轮啮合刚度代表齿轮抵抗变形的能力[12]，由于啮合齿数的变化，齿轮变形处于周期性变化之中，因此齿轮啮合刚度在齿轮啮合周期内并不恒定。齿轮啮合刚度的周期性变化是导致齿轮振动和噪声的原因之一。齿轮单齿的啮合刚度的一般表达式为[13]：
$$ k_n=\frac{\boldsymbol{F}_n}{u_n}\ \ \ n=1,\ 2,\ 3,\cdots $$ (12) 式中：Fn为作用于齿廓面的法向接触力；un为单齿综合弹性形变。
单齿综合弹性形变un的计算式为：
$$ {u}_{n}=\sum _{i=1}^{2}{u}_{Hi}+\sum _{i=1}^{2}{u}_{bi}+\sum _{i=1}^{2}{u}_{fi} $$ (13) 式中：uHi为接触弹性形变；ubi为齿面接触位移；ufi为轴承等的变形对接触位置的影响。
当齿轮处于多齿接触啮合区时，齿轮的综合刚度为各单齿啮合刚度之和，故齿轮的多齿啮合刚度为[14]：
$$ {k}_{m}=\sum _{i=1}^{p}{k}_{ni} $$ (14) 基于扭矩和齿轮转角变形的齿轮啮合刚度计算式为[15]：
$$ k_n=\frac{\boldsymbol{T}}{\theta\cdot r_b^2} $$ (15) 式中：T为齿轮负载扭矩；θ为齿轮转角变形；rb为基圆半径。
由式(15)可得，在对齿轮施加的扭矩已知的情况下，齿轮啮合刚度可以通过求解齿轮转角变形求解。计算齿轮的重合度，如式(16)所示[16]：
$$ \varepsilon =\frac{\left[{Z}_{1}\left(\mathrm{tan}\;{\alpha }_{1}+\mathrm{tan}\;\alpha \right)+{Z}_{1}\left(\mathrm{tan}\;{\alpha }_{2}+\mathrm{tan}\;\alpha \right)\right]}{2\text{π} } $$ (16) 式中：Z1为大齿轮齿数；Z2为小齿轮齿数；α为啮合角度；α1为小齿轮齿顶圆压力角；α2为大齿轮齿顶圆压力角。
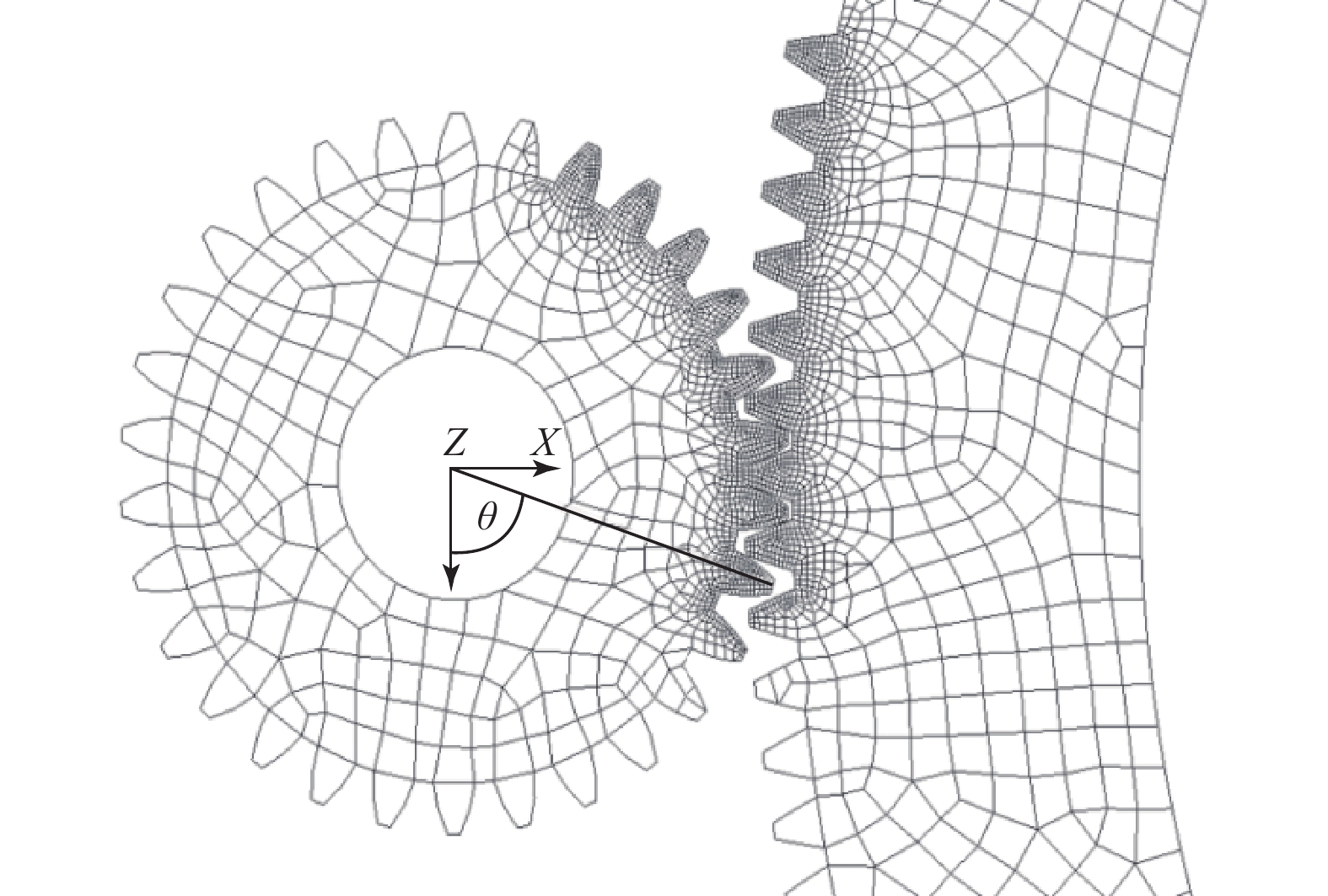
旋转角度示意如图9所示，齿轮的啮合按照双齿啮合—单齿啮合—双齿啮合的顺序交替进行。
在每个啮合区间选取5个啮合位置，对各个位置的齿轮转角变形Δθ进行求解。将通过测量得到的各个啮合位置的齿轮转角变形代入式(15)进行计算，即可得到不同齿轮转角变形量下的啮合刚度，计算结果如表5所示。
表 5 不同齿轮转角变形量下的啮合刚度Table 5. Meshing stiffness values under different gear angle deformations啮合状态 旋转角度
θ/rad齿轮转角变形
Δθ/(10−3rad)啮合刚度
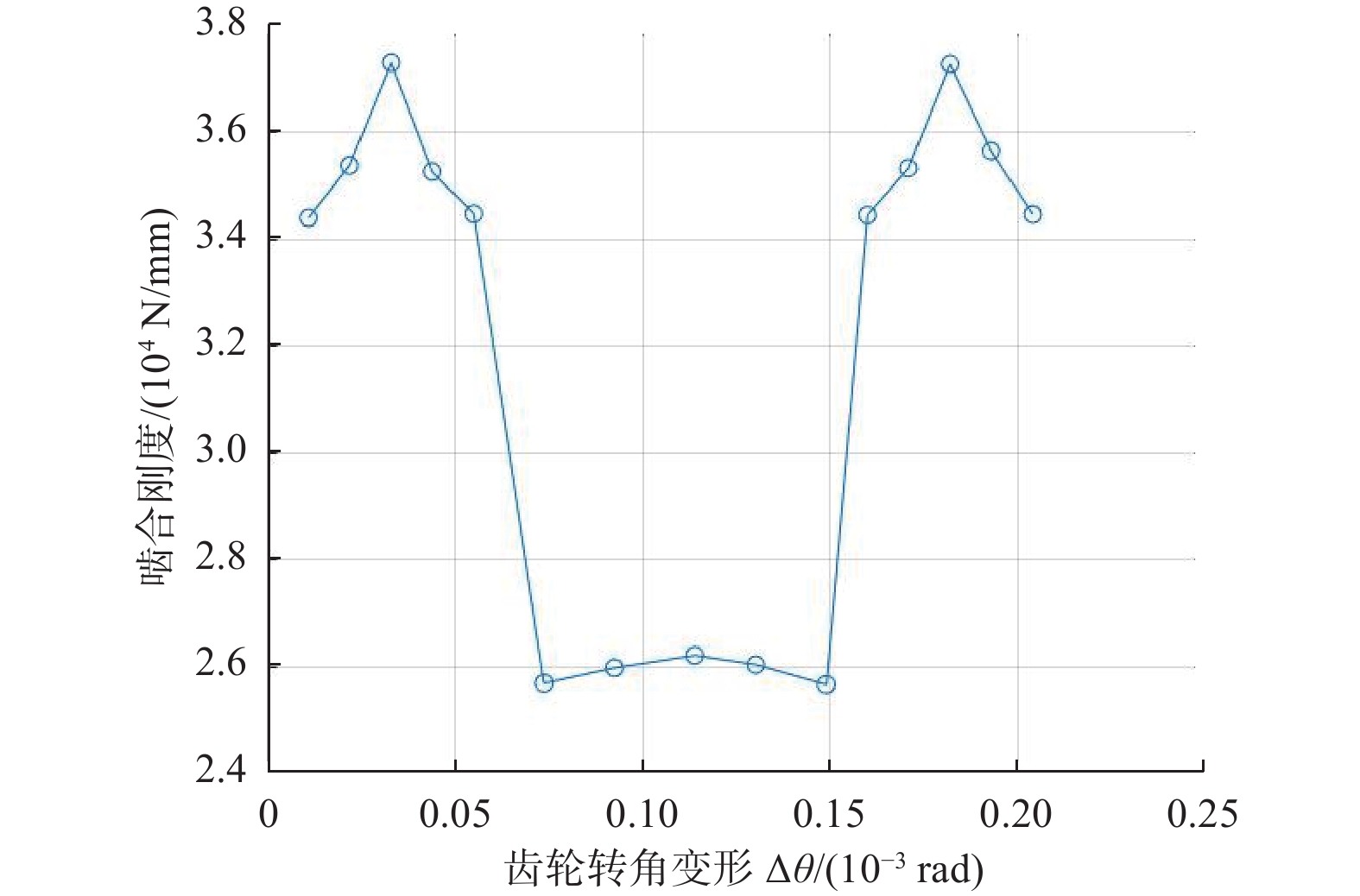
/(104N/mm)双齿啮合 0.011 0.011 3.44 0.022 0.022 3.538 0.033 0.033 3.73 0.044 0.044 3.5265 0.055 0.055 3.4475 单齿啮合 0.0738 0.0738 2.57 0.0926 0.0926 2.5985 0.1114 0.1114 2.622 0.1302 0.1302 2.6045 0.149 0.149 2.5675 双齿啮合 0.160 0.16 3.445 0.171 0.171 3.533 0.182 0.182 3.7275 0.193 0.193 3.595 0.204 0.204 3.4465 图10是利用MATLAB绘制的不同齿轮转角变形下的齿轮刚度变化曲线。由图10可知，齿轮啮合区刚度先增大后减小，呈拱形分布，在齿轮啮合过程中，啮合刚度呈周期性变化[17]。齿轮在双齿啮合区时，载荷由两对齿轮共同承担，齿轮抵抗变形能力强，所以双齿啮合区的刚度比单齿啮合区大。齿轮在啮入与啮出时，刚度会发生较大幅度变化，因为齿轮在啮合过程中会出现齿顶干涉现象，造成齿顶处应力集中，使刚度发生较大幅度变化。
![]()
图 10 不同齿轮转角变形下的齿轮刚度变化曲线Figure 10. Gear stiffness variation curve under different gear rotation angle deformation3. 结论
针对放射治疗设备运动系统的C形臂结构通过转床方式实现非共面照射存在的操作复杂且有安全隐患，本文设计了一种将旋转机架与多轴运动机械臂相结合的球面放疗加速器运动系统结构设计方案。相对于C形臂，该设备可以实现α转角30°的非共面照射，空间利用率约为40%，相对提高了4%[18]。
针对赛博刀只能实现半球定点照射且无法高效拉弧照射的问题，本文提出了一种在治疗过程中治疗床保持不动，由旋转机架带动多轴运动机械臂旋转，多轴机械臂带动束流模块和MLC模块运动的方案，该方案高效地实现了射束既可用于体部又可用于头部的非共面照射。
针对放射治疗设备精度要求极高、设备运行过程中需保持高度稳定的特性，本文采用双平面配重法对所设计的放射治疗设备进行动平衡设计。配重后，设备整体质量小于7 t，在运行过程中不会出现旋转偏移现象。然而，由于设备整体尺寸较大，因此对治疗室空间要求较高。
针对齿轮的特性，为了保证齿轮在实际使用过程中的可靠性，本文对齿轮进行了强度校核和刚度分析，确保其具有足够的承载能力。目前已做出样机待投入临床使用后进行改进。
-
![]()
图 8 齿轮副部分啮合位置等效应力云图
Figure 8. Equivalent stress cloud diagram of partial meshing position of gear pair
![]()
图 10 不同齿轮转角变形下的齿轮刚度变化曲线
Figure 10. Gear stiffness variation curve under different gear rotation angle deformation
表 1 部分部件的质量及旋转半径
Table 1 Weight and radius of rotation of some parts
序号 部件名称 质量/kg 旋转半径/mm 角度/(°) 1 平板探测器 26.3 607.45 29 2 脉冲调节器 137 1032.44 14 3 球管支架组1 34.9 963.36 330 4 高压控制箱1 26 1130.88 316 5 屏蔽体 872 661.37 271 6 栅控枪及电源 5 1255.5 136 7 束流模块 381 902.31 86 
下载: 导出CSV
表 2 部分齿轮参数
Table 2 Parts of gear parameters
齿轮 模数 齿数 压力角
/(°)齿顶圆
/mm齿根圆
/mm分度圆
/mm小齿轮 8 30 20 256 220 240 大齿轮 8 180 20 1456 1420 1440
下载: 导出CSV
表 3 齿轮在不同时间下的最大接触应力
Table 3 Maximum contact stress of gear at different time
单位：MPa 时间/s 0.2465 0.5015 0.7465 0.9851 模型a 75 260 380 162 模型b 62 254 370 192 模型c 68 225 357 197
下载: 导出CSV
表 4 齿轮各啮合位置最大接触应力
Table 4 Maximum contact stress at each meshing position of gear
单位：MPa 图号 a b c d e f 啮合位置 单齿 啮入 双齿 双齿 啮出 单齿 最大接触应力 172 326 72 48 398 126
下载: 导出CSV
表 5 不同齿轮转角变形量下的啮合刚度
Table 5 Meshing stiffness values under different gear angle deformations
啮合状态 旋转角度
θ/rad齿轮转角变形
Δθ/(10−3rad)啮合刚度
/(104N/mm)双齿啮合 0.011 0.011 3.44 0.022 0.022 3.538 0.033 0.033 3.73 0.044 0.044 3.5265 0.055 0.055 3.4475 单齿啮合 0.0738 0.0738 2.57 0.0926 0.0926 2.5985 0.1114 0.1114 2.622 0.1302 0.1302 2.6045 0.149 0.149 2.5675 双齿啮合 0.160 0.16 3.445 0.171 0.171 3.533 0.182 0.182 3.7275 0.193 0.193 3.595 0.204 0.204 3.4465
下载: 导出CSV
-
[1] RAVI A, FLORENCE K, FRANCINE E, et al. Contemporary radiotherapy: present and future[J]. The Lancet, 2021, 398(10295): 171-184. doi: 10.1016/S0140-6736(21)00233-6
[2] CHANDRA R A, KACHNIC L A, THOMAS CR J R. Contemporary topics in radiation medicine, part I: current issues and techniques[J]. Hematol Oncol Clin North Am, 2019, 33 (6): I.
[3] 张琪月, 李鸿岩, 张红, 等. 人工智能在肿瘤放射治疗中的应用[J]. 中华肿瘤防治杂志, 2024, 31(3): 173-180,186. [4] ROSENBLATT E, ZUBIZARRETA E. Radiotherapy in cancer care: facing the global challenge[M]. Vienna: International Atomic Energy Agency, 2017.
[5] 工业和信息化部, 国家卫生健康委员会, 国家发展和改革委员会, 等. 关于印发“十四五”医疗装备产业发展规划的通知(工信部联规〔2021〕208号)[EB/OL]. (2021-12-21)[2024-04-27]. https://www.miit.gov.cn/cms_files/filemanager/1226211233/attach/20224/36c16383a46b4305b38ab8640f24486c.pdf. [6] HOFFMANN A, OBORN B, YAN S, et al. MRI-guided proton therapy: a review and a preview[J]. Radiat Encology, 2020, 15129: 13.
[7] 朱志强, 程鹏, 陈刘利, 等. 医用电子直线加速器技术现状与发展趋势[J]. 中国医疗器械杂志, 2024, 48(2): 184-191. doi: 10.12455/j.issn.1671-7104.230390 [8] 刘会英, 李微微, 柴培林, 等. 机械臂重力平衡机构的设计与实验研究[J]. 机械设计与制造, 2019(11): 44-46,50. [9] 章恒, 干蜀毅, 胡戎兴, 等. 基于SolidWorks二次开发的螺杆转子动平衡自动计算设计[J]. 真空科学与技术学报, 2023, 43(6): 487-493. [10] 滕文爽, 郭梅, 宋振海. HB与ISO锥齿轮齿面接触疲劳强度计算标准比较[J]. 机械传动, 2021, 45(4): 156-159,176. [11] 刘怀举, 陈地发, 朱才朝, 等. 齿轮弯曲疲劳的研究进展与发展趋势[J]. 机械工程学报, 2024, 60(3): 83-108. [12] 刘子谦, 孙宇, 周朝东, 等. 斜齿轮啮合刚度改进算法及其影响因素分析[J]. 机械传动, 2023, 47(3): 39-48. [13] 陈思宇, 谭儒龙, 郭晓东. 直齿锥齿轮啮合刚度计算方法研究[J]. 机械传动, 2021, 45(9): 62-67. [14] 樊智敏, 江峰, 马瑞磷, 等. 基于有限元法的双渐开线齿轮啮合刚度计算[J]. 机电工程, 2021, 38(2): 151-157. doi: 10.3969/j.issn.1001-4551.2021.02.003 [15] 黄一伦, 陈旭, 胡玉梅, 等. 考虑中心距偏差的直齿轮啮合刚度及振动分析[J]. 机械科学与技术, 2024: 1-16. [16] 陈思宇, 谭儒龙, 郭晓东, 等. 直齿圆柱齿轮啮合刚度计算方法研究[J]. 重庆理工大学学报(自然科学), 2021, 35(1): 97-103. [17] 魏永峭, 郭瑞, 刘永平, 等. 变双曲圆弧齿线圆柱齿轮时变啮合刚度和传动误差分析[J]. 华中科技大学学报(自然科学版), 2023, 51(12): 73-82. [18] ROSENBERG I. Radiation oncology physics: a handbook for teachers and students[J]. Br J Cancer, 2008, 98: 1020. doi: 10.1038/sj.bjc.6604224
计量
- 文章访问数: 26
- HTML全文浏览量: 4
- PDF下载量: 9
